Teorie chaosu a s ní související fraktální geometrie jsou velmi mladé obory. K jejich vzniku významně přispěly počítače. Práce mnoha vědců s chaosem byla a je založena na prozkoumávání mnoha grafů spočítaných sice velmi jednoduchými rovnicemi, ale zato s velkou přesností. A právě k tomu se velmi dobře hodí počítače.

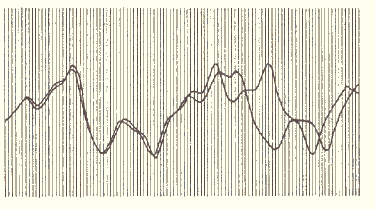
Na přelomu padesátých a šedesátých let se mnoho vědců zabývalo předpovědí počasí. Edward Lorenz nebyl sice meteorolog, ale počasí ho velice zajímalo. Byl jedním z mála šťastných vědců, kteří měli ke své práci počítač. Dlouhou dobu se pokoušel vymyslet rovnice popisující chování atmosféry. V té době byly i výpočty jednoduchých rovnic velmi pomalé a tak si jednou zkrátil čas výpočtem pouze poloviny grafu. Počáteční hodnoty zvolil dle předchozího výpočtu a nechal počítač kreslit graf. Když byl graf hotov srovnal jeho část s již dříve spočítaným grafem a zjistil, že se po chvíli grafy rozcházejí a odlišují se. Původně si myslel, že to je chyba jeho počítače, ale i po opětovném výpočtu se dostavil stejný efekt. Po nějaké době zjistil, že počítač počítá s osmi desetinnými místy, ale on jich zadal pouze šest. Tehdy si uvědomil, že předpovídat počasí není tak jednoduché jak se zdálo. Jakkoliv malá nepřesnost při vyjádření počátečních podmínek znamená velou odchylku od skutečnosti. Tato velmi důležítá myšlenka se neprojevuje pouze u počasí, ale i u naprosté většiny chaotických systémů.

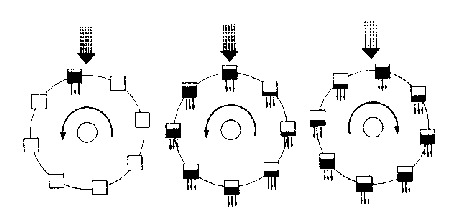
Další Lorenzova práce označovaná jako "zázračný článek" se týká chování vodního kola, kde do nádob na něj připevněných postupně přitéká a odtéká voda. Celý proces vypadá jako velmi jednoduchý, ale není tomu tak. Jedná se o první slavný chaotický systém. Voda stéká do horní nádoby a ta po naplnění vlivem gravitace roztočí kolo. Jenže co když se nádoba nestačí naplnit celá a vlivem setrvačnosti se kolo zastaví? Nebo se naopak roztočí na druhou stranu? Lorenz si tedy několika lineárními rovnicemi vyjádřil chování vodního kola a nechal počítač zobrazit graf. Očekával buď že se kolo bude otáčet stále jedním směrem, nebo se bude periodicky střídat otáčení na každou stranu. Jenže Lorenzův systém neudělal ani jedno.

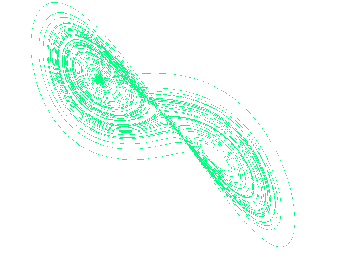
Díky zvoleným hodnotám se systém dostal do nestability, kdy nebylo jasné jak se bude v příštích okamžicích chovat. Na obrazovce jeho počítače se objevila 3D mapa zobrazující chování vodního kola. Kdyby se křivka protla, znamenalo by to cyklické opakování děje. To se ale kupodivu nestalo. Místo toho se objevila nekonečná křivka v prostoru připomínající motýlí křídla. V té době ovšem Lorenz netušil, že se jedná o fraktál. Ta se stala symbolem chaosu a naleznete ji snad v každé knize o tomto oboru.

Na nějakou dobu zůstal Lorenz zapomenut a mezi vědci nepochopen. Až v roce 1972 objevil jeden matematik jeho článek a věnoval jej Jamesi Yorkemu. Pro Yorkeho práci měl velký význam. Uvědomil si, že není možné na všechny věci nahlížet jako na lineární. Článek na něj udělal velký dojem a tak jeho fotokopie rozdával svým přátelům. Jednu kopii věnoval také Stevu Smaleovi z Univerzity v Berkeley a na papír napsal své jméno, aby mu ji vrátil. Smale podobně jako Yorke objevil v článku velmi zajímavé a revoluční myšlenky a situace se opakovala - fotokopii věnoval každému kdo byl ochoten si je vzít. Jenže na fotokopiích bylo Yorkeho jméno a adresa, takže vznikl dojem že Lorenze objevil Yorke. Yorke se ovšem neproslavil pouze touto příhodou. Byl a je jendím z nejvýznamnějších vědců zabývajících se chaosem a dynamickými systémy.

V té době se chaosem začal zabývat také Benoit Mandelbrot. Mandelbrot byl všeuměl. Zabýval se matematikou, vyučoval fyziku, filozofii, fušoval do ekonomie, astronomie a pracoval u IBM. Sám ze sebe udělal postupem času mýtus. Mnoho vědců jej obdivovalo, někteří jej nesnášeli. Jednoho dne se doslechl o problémech inženýrů z IBM. Ti se potýkali s problémem šumu na telefonních linkách mezi počítači. šum se objevoval zcela náhodně a stejně i mizel. Většinou se problém snažili řešit opravou kabeláže, ale to nepomáhalo. Mandelbrot si nechal vytisknout grafy datových přenosů a šumu způsobujících chyby. Po nějaké době našel zajímavou podobnost mezi tzv. Cantorovým mračnem a šumem. Tento obrazec vznikne rozdělením úsečky na tři shodné části a opakováním tohoto procesu na obou krajních dílech. Inženýři to nejprve nedokázali pochopit, ale pokusili se problém vyřešit opakováním přenosu v těchto "zašuměných" částech přenosu dat - a fungovalo to. Mandelbrot dále dospěl k doměnce, že přírodě existuje skrytý fraktální řád. Tato myšlenka se potvrdila prací Michaela Barnsleyho. O tom ale až dále.

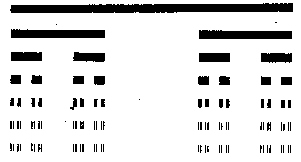
Díky již zmiňovanému měření obvodu Velké Británie se Mandelbrot dostal k mnoha zajímavým otázkám. Kolik dimenzí má klubko provázku? Pokud se na něj podíváte s větší vzdálenosti, je to třírozměrný objekt. Jenže provaz je v podstatě jednodimenzionální přímka omotaná kolem sebe v 3D! Provaz se dále dělí na vlákna a ta se rozpadají v body s nulovou dimenzí. Co je ale mezi těmito dimenzemi? Od kdy je objekt jednodimenzionální, kdy má dimenze dvě? Takto Mandelbrot došel ke zlomkovým dimenzím, které nám umožňují vyjádřit míru nepravidelnosti objektu. Tento objev vedl nakonec k dnešní definici¹ fraktálů a umožnil snadno popsat "fraktálnost" objektů.

Asi nejslavnější prací Mandelbrota je objev tzv. Mandelbrotovy množiny. Ta se stala symbolem všech fraktálů, podobně jako Lorenzův atraktor je symbolem teorie chaosu. Lidé si ji oblíbili především z estetických důvodů. O tom ale až v kapitole o Mandelbrotově množině.