Hausdorfova - Besicovitchova dimenze D udává míru nepravidelnosti útvaru. Pro fraktální objekty je číselná hodnota této dimenze větší než hodnota dimenze topologické. Ne-fraktální objekty mají tu vlastnost, že zmenšováním délky měřidla se přibližuje délka objektu (obvod) k nějaké limitní hodnotě. U fraktálů to neplatí, délka se neustále zvětšuje. Tato vlastnost se nazývá Richardsonův efekt.

Představte si, že máte rozdělit úsečku o délce jedné jednotky na pět stejných dílků. Délka jednoho dílku bude tedy r = 1/5. Počet dílků označme jako N, po zobecnění to bude r = 1/N. Když budeme místo úsečky dělit čtverec na 25 dílků, vzoreček bude vypadat stejně r=1/5. Zde po zobecnění je ovšem r=1/N^1/2. Podobně u krychle bude obecný vzorec vypadat r=1/N^1/3. Je možné zapsat obecný výraz

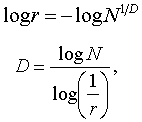
U geometricky pravidelných objektů je výpočet dimenze jasný. Co se ale stane když tento vzorec použijeme na fraktál? Můžeme vyzkoušet nejjednodušší fraktál, kochovu křivku:

Při každé transformaci se délka na (r =) 1/3 své původní hodnoty a počet samopodobných úseků N = 4. Můžeme tedy dosadit do vzorečku D = log 4 / log 3 = 1.2618. Jak je vidět, výsledkem je fraktální dimenze objektu.

Tímto vzorcem je možné určovat jak u symetricky pravidelných těles topologickou i u fraktálů Hausdorfovu-Besicovitchovu dimenzi. Tím také slouží k rozlišení fraktálů a geometricky pravidelných těles. Stejně jej můžeme aplikovat na každý fraktál.