Fraktály, o kterých jsem se zmínil v předchozích kapitolách, představují jen jejich nepatrný zlomek. Vznikly stovky - nebo možná spíš tisíce - fraktálů. Některé jsou uměle vykonstruované, jiné zobrazují jinak nepochopitelné přírodní děje. Mezi ně patří například turbulence, která bez teorie chaosu nebyla pochopitelná.
Asi nejznámnější chaotický fraktál je Lorenzův atraktor. Vznikne zapsáním rovnic popisujících chování vodního kola (viz 2. kapitola). Matematicky zjednodušeno se dá zapsat také takto:
yn = yn-1 + d * (xn-1 * (c - zn-1) - yn-1)
zn = zn-1 + d * (xn-1 * yn-1 - b * zn-1)

Další fraktál nazývaný dle jeho jména autora Hénonův atraktor. Vznikne natahováním a ohýbáním fázového prostoru. Hénon si jej původně kreslil ručně na papír a výpočty dělal na kalkulačce. Při takto pomalém výpočtu je vidět, že body atraktoru se objevují "náhodně" a nakonec vytvoří takovýto útvar.
Přestože je tento atraktor tak jednoduchý, představuje pro matematiky stále problém. Při postupném zjemňování fraktálu se objevují nové a nové detaily a ukazuje se, že jednotlivé křivky nejsou pouze křivkami, ale nekonečně mnoho párů křivek "vedle" sebe. Přesto není možné bez výpočtu určit, kde se následující atraktoru bod objeví.
Výpočet tohoto fraktálu je opravdu velmi jednoduchý:
yn = 0.3 xn-1

Samozřejmě existují i fraktály, které vznikly z čistě estetického hlediska. Příkladem je fraktál nesoucí jméno King's dream. Vymyslel jej Clifford Pickover a poprvé byl uveřejněn v knize Chaos in Wonderland. Jeho výpočet je také velice snadný:
yn = sin(xn-1 a) + d sin(yn-1a)
a,b,c a d jsou konstanty. Na jejich vhodném zvolení závisí tvar fraktálu. Použité hodnoty jsou a=-0.966918, b=2.879879, c=0.765145, d=0.744728.

Nejvíce fraktálů vymyslela ovšem příroda. Velice zajímavé útvary tvoří různé oscilátory. Ve většině případů vznikají očekávané obrazce, ovšem při vhodném zvolení počátečních podmínek se stávají věci které nikdo nepředvídal.
 |
 |
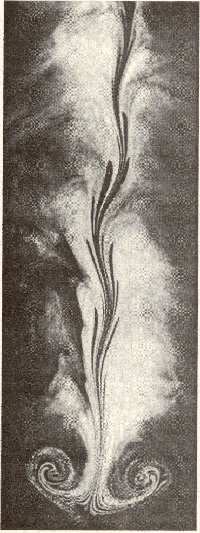
Nejen oscilátory mají v některých případech chaotické chování. Dalším příkladem je turbulence či různé chemické reakce. Pěkné obrazce vzniknou také protažením tyče ve vazké tekutině. Pokud tyč protáhneme jednou, vznikne jednoduchý vlnitý obrazec. Pokud ji protáhneme víckrát, vznikají komplikovanější útvary.
 |
 |
Po dlouhou dobu se mnoho matematiků a biologů zabývalo fraktály u nihž známe matematické vyjádření a zobrazí nám nějaký objekt známý ze života. Existují fraktály, které "nakreslí" hlávku zelí či bláto. Michael Barnsley se zabýval procesem opačným, tedy jak nalézt u neznámého fraktálu jeho matematické vyjádření. Přišel na velice jednoduchou metodu. Nazval ji kolážová věta a funguje zhruba takto: Nakreslíte si útvar, který chcete reprodukovat. Ten "pokladete" zmenšenými kopiemi, které se mohou dokonce i ledabyle překrývat (!!). Vysoce fraktálové útvary se "dláždí" snadno, u méně fraktálových útvarů je to obtížnější. Při zanedbání drobného zkreslení to je ale možné u všech. Pokud je obrázek složitý, budou složitá i pravidla. Na druhou stranu pokud je obrázek fraktálem, budou pravidla velmi jednoduchá. A vzhledem k tomu že jeden z hlavních poznatků Benoita Mandelbrota je že v přírodě fraktálový řád je, nebude problém u přírodních struktur tuto informaci dekódovat. Vždyť i DNA musí obsahovat jen velmi malé množství informací, ze kterého vyroste velmi složitý jedinec.
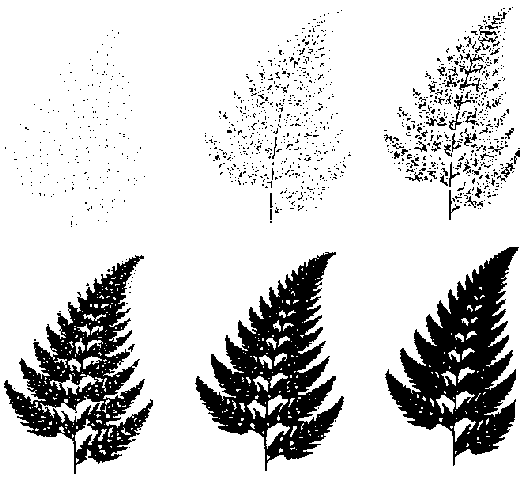
Vzhledem k tomu, že Barnsley měl rád kapradiny, vybral si je pro své některé experimenty. Pomocí počítačového terminálu a myši pokladl kapradinu malými kopiemi sebe sama. A výsledek vidíte na obrázku.