Mezi nejjednodušší fraktály patří tzv. IFS, neboli iterační funkční systémy. Nejjednodušší je vysvětlit princip IFS na jednom z nejjednodušších fraktálů - Kantorově diskontinuu. Na počátku je přímka. Tu rozdělíme na tři shodné části. A obě krajní části zase rozdělíme na tři části, na které aplikujeme toto pravidlo. Nejprve vznikne několik úseček, ale ty se postupně změní v malé tečky. Po nekonečně mnoho opakováních vznikne jen nekonečně mnoho bodů. Je téměř podivuhodné, že i takto jednoduchý obrazec je fraktálem. Ale je tomu skutečně tak.

Dalším jednoduchým fraktálem je Kochova vločka. Představte si trojúhelník, k jehož každé straně "přilepíme" k prostřední třetině další trojúhelník o třetinu menší. A tento postup budeme opakovat i na tento trojúhelníček. Po mnoha opakováních vznikne křivka s několika velice zajímavými vlastnostmi, které nalezneme i u dalších fraktálů. Tato křivka nikdy neprotne sebe sama, neboť nové trojúhelníky jsou příliš malé, než aby si "překážely". Každá iterace křivku o malý kousek prodlouží, ale plocha zůstává na rozdíl od křivky konečná.

Velice známý fraktál je Sierpinského trojúhelník. Tento obrazec vznikne tak, že z trojúhelníka vyřízneme trojúhelník tvořený středními příčkami trojúhelníka původního. A tento postup opakujeme na tři zbylé trojúhelníčky. Tím vznikne nekonečně mnoho nekonečně malých trojúhelníčků.

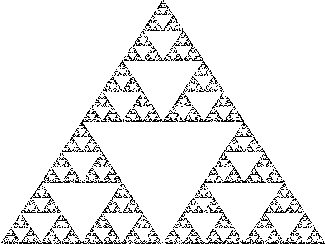
Nemusíme se pouze omezovat na trojúhelníky či jiná dvojrozměrná tělesa. Můžeme vyřezávat třeba z obdélníku. Tím vznikne další fraktál, Sierpinského koberec. Pokud budeme provádět podobné operace na třírozměrné objekty, vzniknou také velice pěkné fraktály. Příkladem je Mengerova houba, trojrozměrná mřížka s nekonečně velým povrchem, ale nekonečně malým objemem.

Podobně je možné pokračovat a nalezli bychom další možná dosud neobjevené fraktály. Vznikla by různá těsnění, křivky, koberečky a další zajímavé útvary.